Invention Coach:
Main Link:
Motivation:
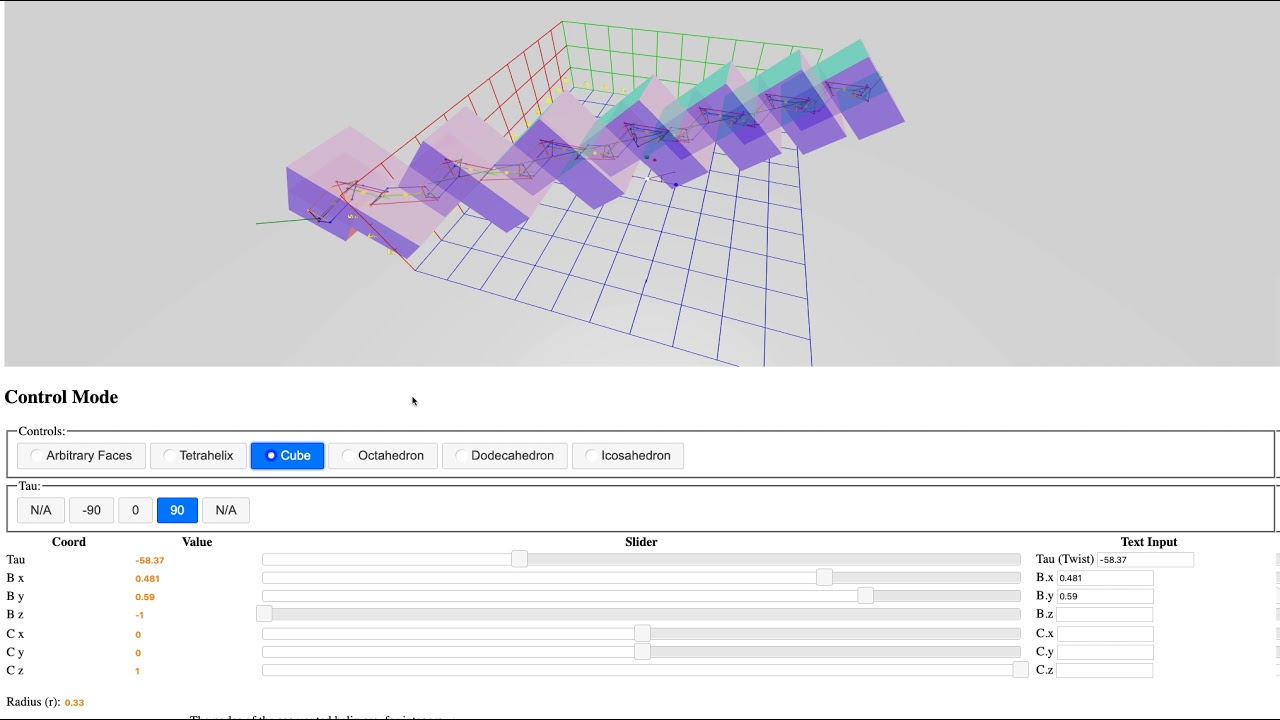
The Search for Helices
The idea that a series of stacked physical objects, such as the Platonic solids, can generate helices, has been published in scattered papers. However, the math to determine the radius and rate of rotation from the underlying object has never been studied. We have proved Eric Lord’s observation based on Chasles’ Theorem, and provided algorithms which allow us to complete, enumerate, and interactively render in 3D, the set of 28 unique Platonic helices.
Use-Cases for the Software
This work allows chemists and mechanical engineers to relate the shape of basic objects to the helices they will produce when strung together, allowing the user to either deduce the objects from the helix or design a desired helix.
Story:
Repeated Objects, and Discovering Helices
During the 2018 Public Invention Mathathon, the participants noticed that every repeated rule led to a physical structure resembling a helix. Following up on this observation led us to our first inklings that all objects produce helices. Over several months we did the research to produce a fully interactive 3D rendering system that allows one to explore this relationship mathematically. Along the way, this net caught the variety of all possible Platonic helices. The team has since published a research paper on the topic.
Related Open-Source Projects
If interested in learning more about our other projects, check the following pages for updates and volunteer opportunities:
Status:
Collateral
Main Interactive Page: https://pubinv.github.io/segmented-helixes/index.html